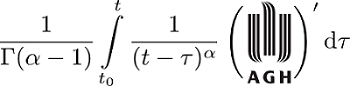Topic

The project focus is on design and application of non integer order controllers, filters, correctors and other control loop elements that would be beneficial for control tasks.

Main objectives of the project are following:

1. Design of methods of approximation and discretisation of non-integer order system that would allow efficient implementation,
2. Analysis of behaviour of non integer order subsystems in control loops, especially of nonlinear systems. In particular stability is one of the interests,
3. Obtaining performance indexes and possibly tuning rules for non integer order controllers and filters that would be efficient and potentially useful,
4. Application of non integer order systems in control loops for real time control.

Along with these objectives certain research questions need answering. In particular is it possible to effectively use Lyapunov-like method for stability analysis of control systems with non integer feedbacks? Moreover are there certain classes of systems where application of non integer order feedbacks is especially beneficial? Are non integer order systems are suitable for real time control, especially with time critical regimes? Is it possible to use classical performance indices such as integrated absolute error and integrated square for optimisation of systems with non integer order feedbacks? These indices should be interpreted as norms in L₁[0,+∞) and L₂[0,+∞), it is not known if solutions of systems with non integer order feedbacks belong to those spaces.

The expected outcome is realisation of majority of these objectives along with positive answer to most of the listed questions. Regarding last question if answer would be negative then construction of appropriate performance index is desired. With questions regarding Lyapunov like methods and determination of special classes there is always a risk of not conclusive answer.